A consistent Hash Ring is a widely used technique in distributing and load-balancing data or operational workload across multiple system components with high fault tolerance. This technique allows distributed shared data to be reaccessed without needing another indexing or discovery component. It enables the remaining components, referred to as nodes, to manage their data by minimizing data relocation when hardware in the system becomes unavailable. This method forms the load-balancing mechanism of applications such as Dynamo DB, HAProxy.
Consistent Hashing Explained
As the size of the data to be stored or the operational workload on the system increases, it is not feasible to handle this amount with a single physical hardware, and the need for managing the load across multiple hardware components, i.e., horizontal scaling, arises. In addition, distributed data or workload shared across multiple components in a distributed system should be accessible by clients with minimal effort. For instance, in a NoSql database, accessing randomly distributed data on multiple nodes would require querying each system component one by one, resulting in a linear time-complexity in the number of added hardware to the discovery operation. This is not a desired approach. One solution to optimize the linear characteristic of the discovery operation is to introduce an external indexing component which tracks the nodes on which the data reside but it is not the only solution. Functions that yield the same result for a specific input can eliminate the need for external component usage for indexing and discovery. For example, hash functions can be used for this purpose.
Hash functions have the property of consistently mapping a random number of elements in the input space to a finite output space, where these elements of the set are called buckets. In other words, for each input x, hash(x) = y, the number of elements in the function’s result set is determined. Using this property, for example, we can map the keys of data sets in a cache or database to the elements of the hash function’s result set. Then, in the next step, we can reduce the resulting value to the desired number of nodes without breaking the mapping consistency by applying the modulus operation. As an example, let A = {1a24d21, c12d422, …, 1e14e124a21} be a key set for which a hash function’s value set is defined such that h(x) = y, for x ∈ A, y = {1, 2, …, 1024}, meaning that for each element in set A, the hash function returns a value up to 1024. If the data to be stored is distributed across four nodes, by applying the modulus operation to the result set, z = y mod 4, we obtain the desired node index, and h(“AB56CD”) = 5, 5 mod 4 = 1, indicating node number 1.
The above example is actually one approach to implement consistent hashing by using hash and modulus functions. If we visualize this implementation, we can imagine that the elements of the hash result set are arranged on a circle and the circle is divided by the nodes which own the before-coming elements:
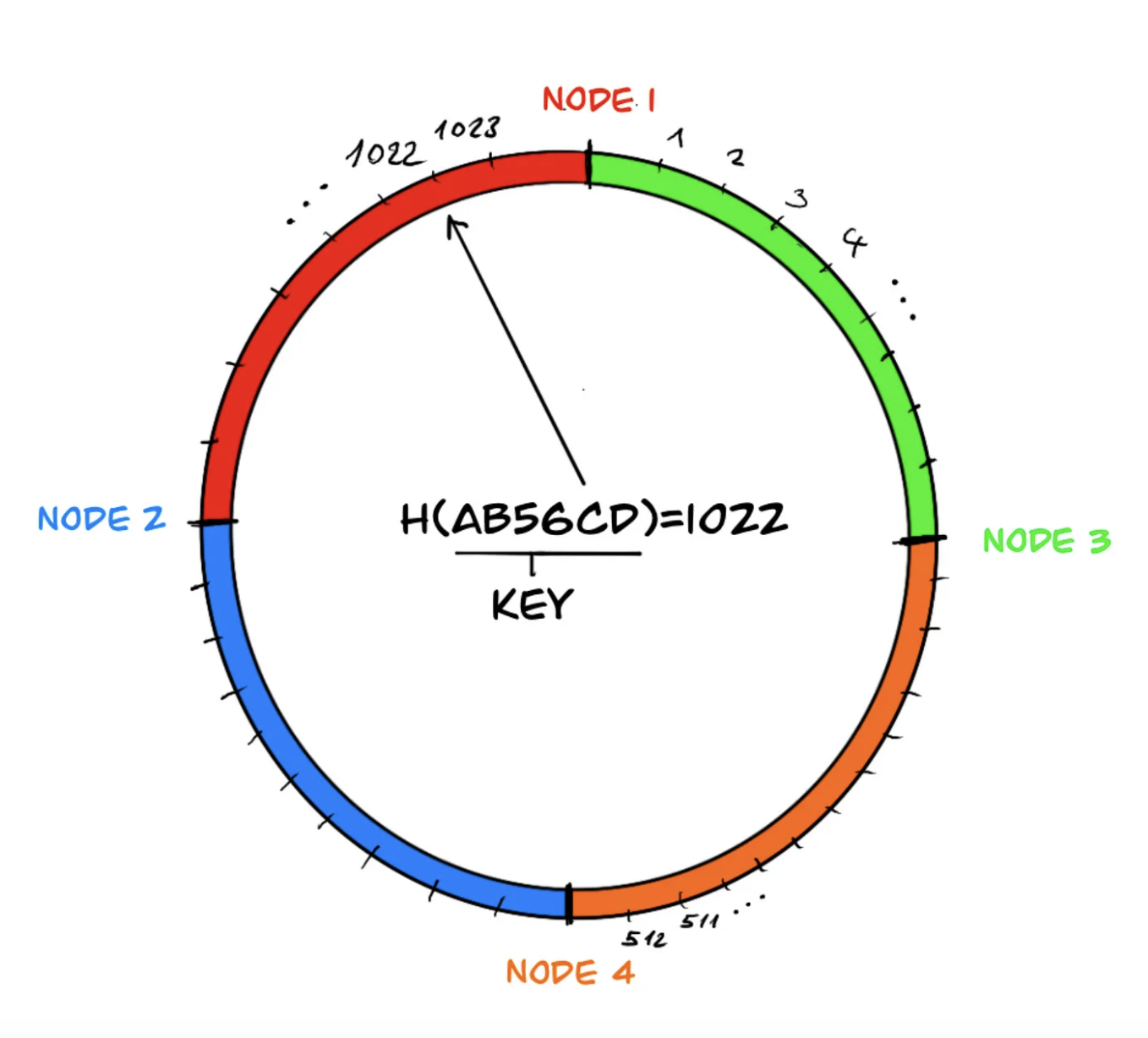
Each differently colored section in the ring defines the key range managed by the nodes, and if we continue moving on the circle beyond the last node area, just like in the modulus operation, we return to the beginning, the first node.
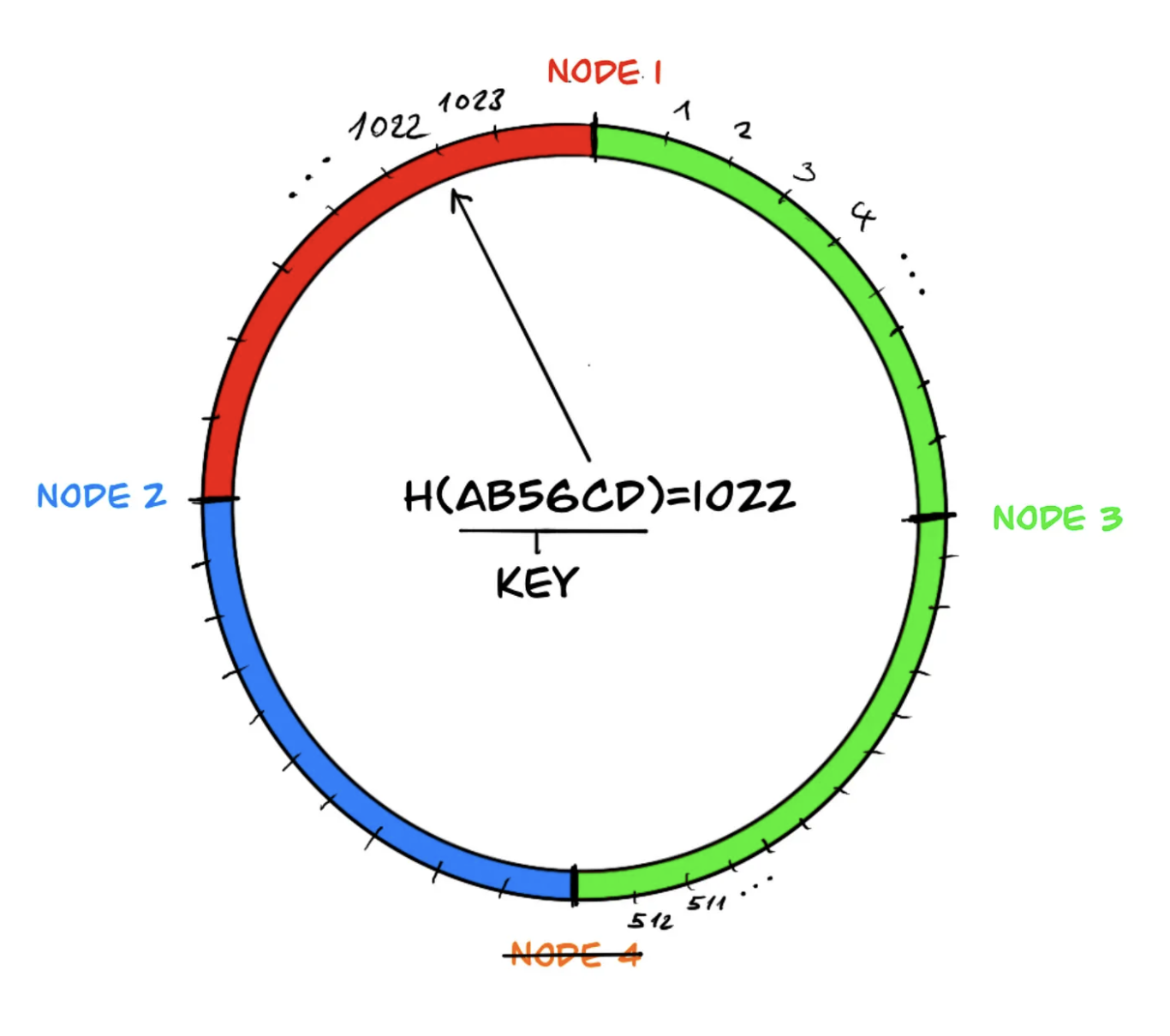
Notice that for a key in the key space, the hash function gives the same output regardless of the number of nodes. If there is a decrease in the number of nodes, the area of the neighboring node responsible for the area of the departed node (in the example, node 4) is merged, eliminating the need for any changes in the data sets managed by the other system components. This way, the impact caused by the departed node does not spread throughout the system and remains local.
Virtual Components
However, in the load distribution mentioned above, the neighboring system component, node 3, may end up with a heavier load during the redistribution of data because it needs to take over the data of the offline component, node 4. To overcome this problem, virtual components are used in the ring, and the distribution of data on the components is rebalanced.

Similarly, if ‘node 4’ leaves the system due to a failure, the data managed by node 4 is more evenly distributed among the remaining three components:
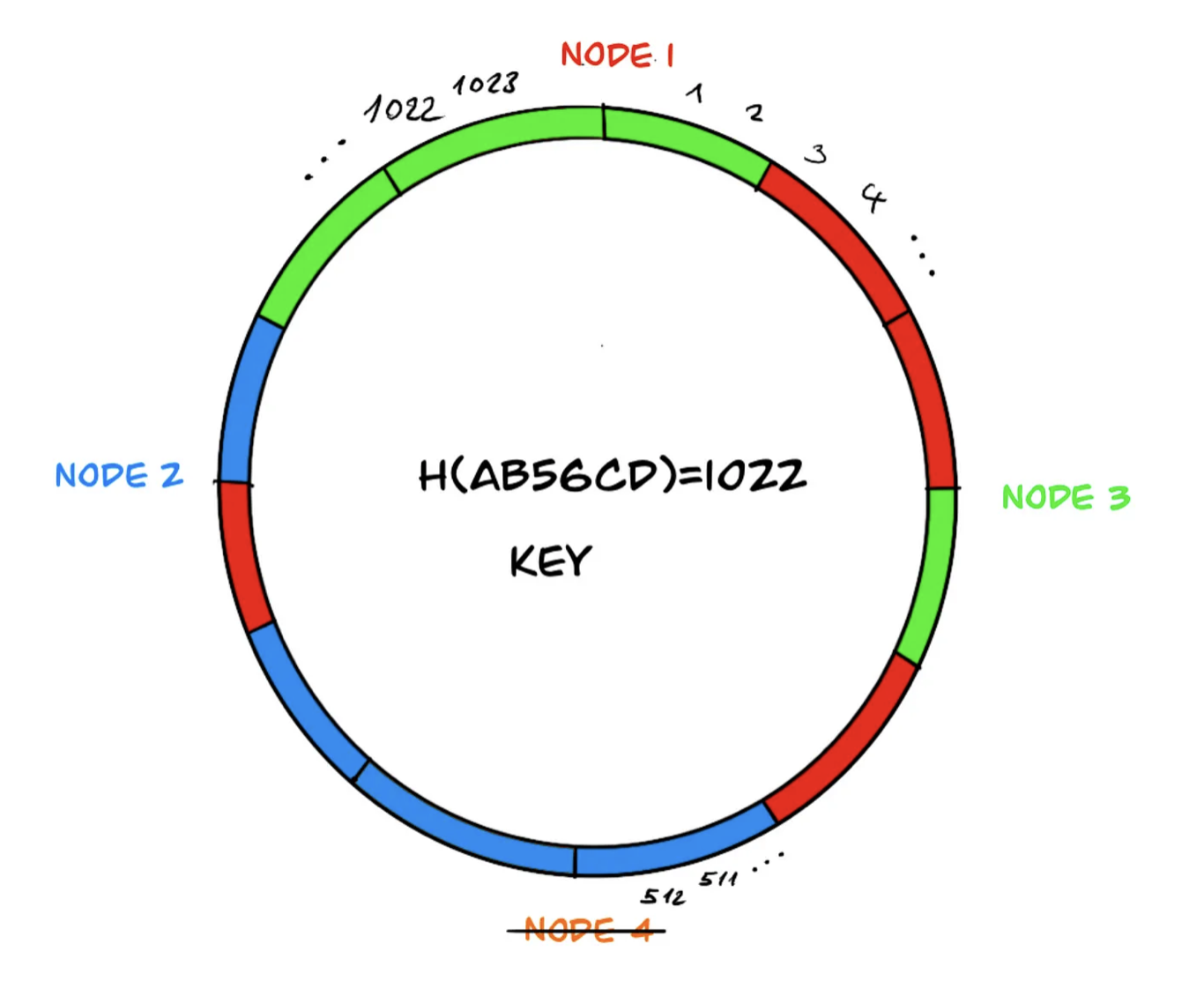
Virtual components are an effective method for balancing the load distribution, but depending on the content of the data, they may not always be sufficient. Therefore, sometimes hotspots and imbalances can occur on the ring. These hotspots are undesirable as they create load imbalances. Despite the addition of virtual components, if there is still an imbalance in the load distribution, a variant of consistent hashing called ‘bounded-load’ can be considered as a solution with an upper limit.
Bounded-Load Hash Ring
In this variant, the capacity upper limits of the ring’s components are predetermined, and if the load exceeds this limit, the incoming load is transferred to the next node with available capacity. This prevents hotspot formation on the nodes. Although this method puts pressure on the ring to prevent hotspot formation, it introduces additional cost when redistributing the data. The decision to use this variant can be made when imbalance is observed in the production load distribution.
In conclusion…
Consistent Hash Ring is a load distribution and balancing technique commonly encountered in database and cache implementations. This method allows us to horizontally scale the data across multiple components and increases fault tolerance as it only requires redistributing the affected data set among the remaining components in case of a node failure. However, depending on the changing number of nodes and the content of the data, the balanced distribution of the load on the nodes can be disrupted by creating hotspots. In such cases, another variant of Consistent Hashing called bounded-load can be used to limit and transfer the overloaded load to the next node.
References
- https://ai.googleblog.com/2017/04/consistent-hashing-with-bounded-loads.html?m=1
- http://highscalability.com/blog/2023/2/22/consistent-hashing-algorithm.html
- https://web.stanford.edu/class/cs168/l/l1.pdf
